Question

The coordinates of the vertices of △RST are R(−3,1), S(−1,4), and T(3,1) .

Which statement correctly describes whether △RST is a right triangle?

△RST is a right triangle because RS¯¯ is perpendicular to RT¯¯ .

△RST is a right triangle because RS¯¯ is perpendicular to ST¯¯ .

△RST is a right triangle because ST¯¯ is perpendicular to RT¯¯.

△RST is not a right triangle because no two of its sides are perpendicular.

Answer 1

The correct answer is:

△RST is not a right triangle because no two of its sides are perpendicular.

Step-by-step explanation:

To determine if any of the sides are perpendicular, we find the slope of the line segment on each side.

The formula for slope is:

`m=(y_2-y_1)/(x_2-x_1)`

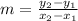
The slope of line segment RS is:

m = (4-1)/(-1--3) = 3/(-1+3) = 3/2

The slope of line segment ST is:

m = (1-4)/(3--1) = -3/(3+1) = -3/4

The slope of line segment RT is:

m = (1-1)/(3--3) = 0/(3+3) = 0/6

If two lines are perpendicular, their slopes are negative reciprocals (opposite signs and flipped). None of these are negative reciprocals, so no two sides are perpendicular.

Answer 2

If the coordinates of the vertices of △RST are R(−3,1), S(−1,4), and T(3,1), then you can consider vectors:


`\overrightarrow{RS}=(x_S-x_R,y_S-y_R)=(-1+3,4-1)=(2,3),\\ \overrightarrow{RT}=(x_T-x_R,y_T-y_R)=(3+3,1-1)=(6,0),\\ \overrightarrow{TS}=(x_S-x_T,y_S-y_T)=(-1-3,4-1)=(-4,3).`

Then check is there any perpendicular two vectors using dot product:


`\overrightarrow{RS}\cdot \overrightarrow{RT}=2\cdot 6+3\cdot 0=12,\\ \overrightarrow{RS}\cdot \overrightarrow{TS}=2\cdot (-4)+3\cdot 3=1, \\ \overrightarrow{RT}\cdot \overrightarrow{TS}=6\cdot (-4)+3\cdot 0=-24.`

Since there are no dot product that is equal to zero, no two of triangle's sides are perpendicular and this triangle has no any right angle.

Answer: Correct choice is D.