Question

How many real-number solutions does the quadratic equation 2x^2 + 7x + 9 = 0 have?

Answer 1

We are given the following equations:

`2x^2+7x+9=0`

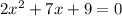
This is an equation of the form:

`ax^2+bx+c=0`

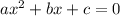
To determine the number and type of solutions we can use the discriminant of the equation. The discriminant is determined by the following number:

`\Delta=b^2-4ac`

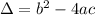
Now, we plug in the values:

`\Delta=(7)^2-4(2)(9)`

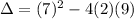
Now, we solve the operations:

`\Delta=-23`

The number and type of solutions are given by the following conditions:

`\begin{gathered} \Delta>0,\text{ two real solutions} \\ \Delta=0,\text{ one real solutions} \\ \Delta=\text{ two complex solutions} \end{gathered}`

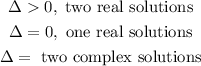
Since we get that:

`\Delta=-23<0`

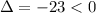
Therefore, the equation has two complex solutions and therefore, no real number solution.