Question

An ideal gas occupies a spherical container of radius 14.5 cm. The temperature of the gasis 179 K, and the pressure is 1.97 atmA) Calculate the radius (in cm) of the container at 3.73 atm and 293 K.

Answer 1

Given data

*The given radius of a spherical container is r_1 = 14.5 cm

*The given temperature of the gas is T_1 = 179 K

*The given pressure is P_1 = 1.97 atm

*The given another pressure is P_2 = 3.73 atm

*The given another temperature is T_2 = 293 K

(A)

The radius (in cm) of the container is calculated by using the relation as

`\begin{gathered} (P_1V_1)/(T_1)=(P_2V_2)/(T_2) \\ \frac{P_1((4)/(3)\pi r^3_1)^{}}{T_1}=(P_2((4)/(3)\pi r^3_2))/(T_2) \\ (P_1r^3_1)/(T_1)=\frac{P_2r^3_2}{T_2^{}} \end{gathered}`

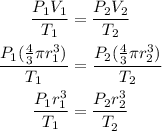
Substitute the known values in the above expression as

`\begin{gathered} (1.97*(14.5)^3)/((179))=\frac{3.73* r^3_{2^{}}}{293} \\ r_2=\text{13}.8\text{ cm} \end{gathered}`

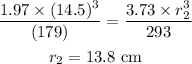
Hence, the radius of the container is r_2 = 13.8 cm