Question

Vector vector v equals vector RS has points R(−2, 12) and S(−7, 6). What are the magnitude and direction of vector RS question mark Round the answers to the thousandths place.

Answer 1

Take into account that vector v can be written as follow:

`\vec{v}=(x-x_o)\hat{i}+(y-y_o)\hat{j}`

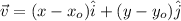
where (x,y) and (xo,yo) are two points on the vector.

In this case, we can use (xo,yo) = R(-2,12) and (x,y) = S(-7,6). By replacing these values into the expression for vector v, we obtain:

`\begin{gathered} \vec{v}=(-7-(-2))\hat{i}+(6-12)\hat{j} \\ \vec{v}=-5\hat{i}-6\hat{j} \end{gathered}`

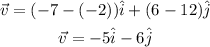
Now, consider that the magnitude of v is the square root of the sum of the squares of the components. Then, we have for the magnitud of v:

`v=\sqrt[]{(-5)^2+(-6)^2}=\sqrt[]{25+36}=\sqrt[]{61}\approx7.810`

Hence, the magnitude of v is approximately 7.810.

Now, consider that the tangent of the angle of the direction of the vector is equal to the quotient between the y component over the x component of the vector:

`\begin{gathered} \tan \theta=(-6)/(-5) \\ \theta=\tan ^(-1)((-6)/(-5))\approx230.194 \end{gathered}`

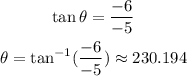
Hence, the direction of vector v is approximately 230.194 degrees.