Answer:
The value of k is -3.
Step-by-step explanation:
To determine the value of k, first, find the equations of f(x) and g(x) using the two-point form of the equation of a line.
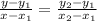
The indicated points on f(x) are (0,1) and (1,-1).
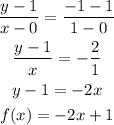
Similarly, the indicated points on g(x) are (1,3) and (0,-3).
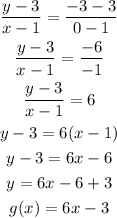
Therefore, we have that:
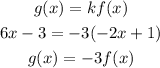
The value of k is -3.