Question

10. The figure shows the graphs of the functions y = f(x) and y = g(x). The four indicated points all have integer coordinates.

Answer 1

The value of k is -3.

Step-by-step explanation:

To determine the value of k, first, find the equations of f(x) and g(x) using the two-point form of the equation of a line.

`(y-y_1)/(x-x_1)=(y_2-y_1)/(x_2-x_1)`

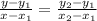
The indicated points on f(x) are (0,1) and (1,-1).

`\begin{gathered} (y-1)/(x-0)=(-1-1)/(1-0) \\ (y-1)/(x)=-(2)/(1) \\ y-1=-2x \\ f(x)=-2x+1 \end{gathered}`

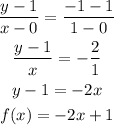
Similarly, the indicated points on g(x) are (1,3) and (0,-3).

`\begin{gathered} (y-3)/(x-1)=(-3-3)/(0-1) \\ (y-3)/(x-1)=(-6)/(-1) \\ (y-3)/(x-1)=6 \\ y-3=6(x-1) \\ y-3=6x-6 \\ y=6x-6+3 \\ g(x)=6x-3 \end{gathered}`

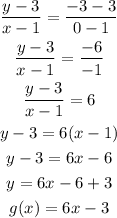
Therefore, we have that:

`\begin{gathered} g(x)=kf(x) \\ 6x-3=-3(-2x+1)_{} \\ g(x)=-3f(x) \end{gathered}`

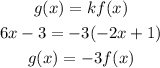
The value of k is -3.