Question

The length of a rectangular field is 20 less than its width. The area of the field is 12,000 ft2. What is the width of the field

Answer 1

its C - 120 ft

Explanation:

on edge 2021

Answer 2

The answer is 120 feet.

The area of the field (A) is:
A = w · l (w - width, l - length)

It is known:
A = 12,000 ft²
l = w - 20
So, let's replace this in the formula for the area of the field:
12,000 = w · (w - 20)
12,000 = w² - 20
⇒ w² - 20w - 12,000 = 0

This is quadratic equation. Based on the quadratic formula:
ax² + bx + c = 0 ⇒
`x= \frac{-b+/- \sqrt{ b^(2)-4ac } }{2a }`

In the equation w² - 20w - 12,000 = 0, a = 1, b = -20, c = -12000
Thus:

`w= \frac{-(-20)+/- \sqrt{(-20)^(2)-4*1*(-12000) } }{2*1} = (20+/- √(400+48000) )/(2) = (20+/-220)/(2)`
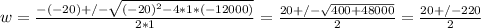
So, width w can be either

`w= (20+220)/(2)= (240)/(2)=120`
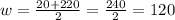
or

`w= (20-220)/(2)= (-200)/(2) =-100`
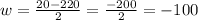
Since, the width cannot be a negative number, the width of the field is 120 feet.