Question

Need help understanding the formula

A juggler is performing her act using several balls. She throws the balls up at an initial height of 4 feet, with a speed of 15 feet per second. If the juggler doesn't catch one of the balls, about how long does it take the ball to hit the floor?

Hint: Use H(t) = _16t2 + vt + s.

7.52 seconds
1.15 seconds
0.47 second
0.22 second

Answer 1

v is the initial speed and s is the initial height so the equation is


`h(t) = -16t^2+15t+4`

Set h(t) equal to 0 and solve for t


`-16t^2+15t+4=0 \\a=-16,b=15,c=4 \\x_(1,2)= (-b \pm √(b^2-4ac))/(2a)= (-15 \pm √(15^2-4(-16)4))/(2(-16))=(-15 \pm √(225+256))/(-32)=(-15 \pm √(481))/(-32) \\x_1=(-15 + √(481))/(-32) \approx -0.22 \\x_1=(-15 - √(481))/(-32) \approx 1.15`

Time must be positive, so the result is 1.15 seconds.

Answer 2

For this case we have the following equation:

`image`

Where,

t: time

v: initial speed

s: initial height

Substituting values we have:

`image`

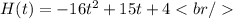
By the time the ball hits the ground we have:

`image`

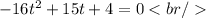
From here, we clear the value of time:

Using the quadratic equation we have:

`t=(-15+/-√(15^2-4(-16)(4)))/(2(-16))`

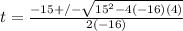
Doing the calculations we have:

`image`

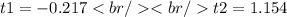
Discarding the negative root, we have that the time is:

`t=1.154`

Answer:

it takes the ball to hit the floor about:

1.15 seconds