Question

Solve the system using the substitution method.

y-3x=2 and y=(x+1)^2-5


Solve the system using the elimination method.
y-3x=2 and y=(x+1)^2-5

Don't exactly understand how to do it either way.

Answer 1

Q1.
y - 3x = 2
y = (x + 1)² - 5

Using the substitution method, we will replace y in the first equation and solve it:
(x + 1)² - 5 - 3x = 2

Since (a + b)² = a² + 2ab² + b², then (x + 1)² = x² + 2·1·x + 1² = x² + 2x + 1
So, let's get back to the equation and replace (x + 1)²:
x² + 2x + 1 - 5 - 3x = 2
x² + 2x - 3x + 1 - 5 - 2 =0
x² - x - 6 = 0

Now use the quadratic formula: ax² + bx + c = 0,
`x = \frac{-b+/- \sqrt{ b^(2)-4ac } }{2a}`
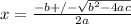
In the equation x² - x - 6 = 0, a = 1, b = -1, c = -6
Thus:

`\frac{-b+/- \sqrt{ b^(2)-4ac } }{2a} =\frac{-(-1)+/- \sqrt{ (-1)^(2)-4*1*(-6) } }{2*1} =(1+/- √( 1-(-24)) )/(2)`
`=(1+/- √( 25) )/(2) = (1+/-5)/(2)`
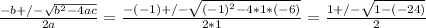
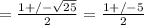
Thus, the solutions are:

`x= (1+5)/(2) = (6)/(2) =3` ⇒
`y = (x+1)^(2)-5=(3+1)^(2) -5=4^(2) -5=16-5=11`

`x= (1-5)/(2) = (-4)/(2)=-2` ⇒
`y=(x+1) ^(2) -5=(-2+1)^(2) -5=(-1)^(2) -5=1-5=-4`

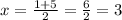
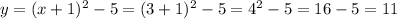
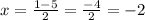
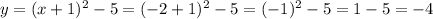
x =3, y = 11 and x = -2, y = -4



Q2.
We have two equations:
y - 3x = 2
y = (x + 1)² - 5
____________
y - 3x = 2
y - (x + 1)² = -5
____________
Let's now, multiply the second equation by (-1):
y - 3x = 2
(-1)·y - (-1)·(x + 1)² = (-1)(-5)
____________
y - 3x = 2
-y + (x + 1)² = 5
____________
Now, add this two equations:
y - 3x + (-y + (x + 1)²) = 2 + 5
y - 3x - y + (x + 1)² = 7

y can be cancelled:
- 3x + (x + 1)² = 7
- 3x + x² + 2x + 1 = 7
x² - x + 1 - 7 = 0
⇒ x² - x - 6 = 0


Now, as in the previous part, use the quadratic formula: ax² + bx + c = 0,
`x = \frac{-b+/- \sqrt{ b^(2)-4ac } }{2a}`
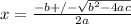
In the equation x² - x - 6 = 0, a = 1, b = -1, c = -6
Thus:

`\frac{-b+/- \sqrt{ b^(2)-4ac } }{2a} =\frac{-(-1)+/- \sqrt{ (-1)^(2)-4*1*(-6) } }{2*1} =(1+/- √( 1-(-24)) )/(2)`
`=(1+/- √( 25) )/(2) = (1+/-5)/(2)`
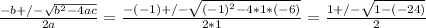
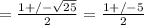
Thus, the solutions are:

`x= (1+5)/(2) = (6)/(2) =3` ⇒
`y = (x+1)^(2)-5=(3+1)^(2) -5=4^(2) -5=16-5=11`

`x= (1-5)/(2) = (-4)/(2)=-2` ⇒
`y=(x+1) ^(2) -5=(-2+1)^(2) -5=(-1)^(2) -5=1-5=-4`

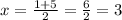
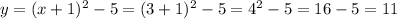
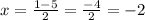
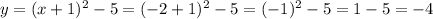
x =3, y = 11 and x = -2, y = -4