Q1. The answer is 7 to the 5 over 4 power
Let's write the fourth root of 7 to the fifth power as a radical. 7 to the fifth power is 7⁵. The fourth root of 7 to the fifth power is
![\sqrt[4]{7^(5) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/n4az0gbjjrl8s5f764y819p6y629jwgvkw.png)
.
Now, to rewrite it as a rational exponent, we will use the following:
![x^{ (m)/(n)}= \sqrt[n]{ x^(m) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/7trg9vuou3cb0g3w95j40167y6r6ydwqwb.png)
Our radical is
![\sqrt[4]{7^(5) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/n4az0gbjjrl8s5f764y819p6y629jwgvkw.png)
which means that n = 4, m = 5.
So, the rational exponent it will be:
![\sqrt[4]{ 7^(5)} =7^{ (5)/(4)}](https://img.qammunity.org/2017/formulas/mathematics/high-school/2qwobzudkyfivs2kvo0p9fma7s32c0x44h.png)
which is the same as 7 to the 5 over 4 power
Q2. The answer is the eighth root of 2 to the fifth power.
Let's present 2 to the 7 over 8 power, all over 2 to the 1 over 4 power as a rational exponent.
2 to the 7 over 8 power is
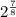
2 to the 1 over 4 power is
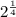
2 to the 7 over 8 power, all over 2 to the 1 over 4 power is
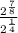
Using the rule:

we have:
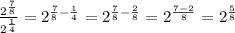
Since:
![x^{ (m)/(n)}= \sqrt[n]{ x^(m) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/7trg9vuou3cb0g3w95j40167y6r6ydwqwb.png)
, then n = 8, m = 5
Therefore
![2^{ (5)/(8) = \sqrt[8]{ 2^(5) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/qknfkvsjjmns0z0jql0y7xt7cgus3rh5rp.png)
Q3. The answer is 9 inches squared.
The area of the rectangle (A) is
A = l · w (l - length, w - width).
It is given:
l = the cube root of 81 inches =
![\sqrt[3]{81}= \sqrt[3]{3^(4) } =3^{ (4)/(3) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/7a6dq0kibb3etauv19jbvr3bw0e4i9et6o.png)
w = 3 to the 2 over 3 =

A =

Since:
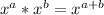
then:
A =
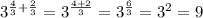
Q4. The answer is By simplifying 25 to 5² to make both powers base five and subtracting the exponents
5 to the fourth power, over 25 = 52 is
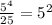
Now, let's simplify 25 to 5²:
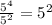
Since

, we will subtract the exponents:
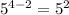
⇒
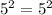
Q5. The answer is the ninth root of 3
3 to the 2 over 3 power is
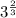
3 to the 2 over 3 power, to the 1 over 6 power is

Since
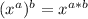
then:

Since:
![x^{ (m)/(n)}= \sqrt[n]{ x^(m) }](https://img.qammunity.org/2017/formulas/mathematics/high-school/7trg9vuou3cb0g3w95j40167y6r6ydwqwb.png)
, then: n = 9, m = 1
![3^{ (1)/(9) }= \sqrt[9]{3^(1) } = \sqrt[9]{3}](https://img.qammunity.org/2017/formulas/mathematics/high-school/ff3znjrk9v5kn6pq3pe5x9t8qrum2612ho.png)