Consider the funcion
 . The dmain of this function is
. The dmain of this function is
 and the range is
and the range is
 .
.
Now if
 you can calculate that
you can calculate that
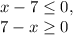
and the function
 will have the domain
will have the domain
 (state this using that expression under the root is
(state this using that expression under the root is
 ).
).
As you can see the x-term inside the radical has a negative coefficient.
Answer: correct choice is D.