Question

How long will it take for a radioactive isotope with a decay constant of 0.15 (which means a half life of 4.6 days ) to decay to 5% of its original value?

(At = A0e^-kt)

A 3 days
B 4.6 days
C 5 days
D 10.73 days
E 19.97 days

Answer 1

E. 19.97 days.

Explanation:

The function that models this situation is

`A(t)=A_(0)e^(-kt)`

This expression models the decay behaviours, where
`k=0.15` is the decay constant.

Now, 5% of its original value refers to
`A(t)=0.05(A_(0))`.

Using all this information in the formula, we have

`A(t)=A_(0)e^(-kt)\\0.05(A_(0))=A_(0)e^(-(0.15)t)\\0.05=e^(-(0.15)t)`

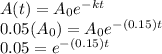
Here, we need to use logarithms to eliminate the power

`ln(0.05)=ln(e^(-(0.15)t))\\ln(0.05)=-0.15t\\t=(ln(0.05))/(-0.15) \approx 19.97`

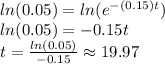
Therefore, the right answer is E. 19.97 days.

Answer 2

we know that N=No exp(-kt), where k is the decay constant, 5% of its original value means N=(5/100)No
so, for t=t', N=(5/100)No, (5/100)No=Noexp(-kt'), (5/100)=exp(-kt')
Ln(5/100)=Lnexp(-kt')= - kt', -2.99 = -0.15t', so t' = 19.93
so the answer is E 19.97 days