Question

A toy boat moves horizontally in a pond. The horizontal position of the boat in meters over time is shown below. Questions: 1. What is the displacement of the boat between 0 s and 16s ? 2. What is the distance traveled by the boat between 0 s and 16s?

Answer 1

1.

The displacement is defined as:

`\begin{gathered} \Delta x=x_f-x_0 \\ \text{ where} \\ x_f\text{ is the final position} \\ x_0\text{ is the initial position } \end{gathered}`

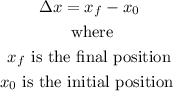
From the graph we notice that the initial position (at t=0 s) is 6 m and the final position (at t=16 s) is -15 m, then we have:

`\begin{gathered} \Delta x=-15-6 \\ \Delta x=-21 \end{gathered}`

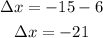
Therefore, the displacement is -21 m

2.

To find the distance traveled by the boat we need to notice that between 0 s and 16 s we have to legs of the motion, then we need to find the distance in each leg and finally we add them to find the total distance traveled in that interval.

To find the distance in each leg we can use the following formula:

`d=\lvert{x_f}-x_0\rvert`

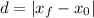
First leg (from 0 s to 8 s).

In this leg of the trip the boat move from 6 m to 15 m, then the distance is:

`\begin{gathered} d=\lvert{15-6}\rvert \\ d=\lvert{9}\rvert \\ d=9 \end{gathered}`

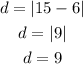
Hence, the boat traveled 9 m in this leg.

Second leg (from 8 s to 16 s)

In this leg of the trip the boat move from 15 m to -15 m, this means that the distance in this leg is:

`\begin{gathered} d=\lvert{-15-15}\rvert \\ d=\lvert{-30}\rvert \\ d=30 \end{gathered}`

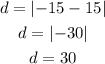
Hence, the boat traveled 30 m in this leg.

Finally, as we said, we just add the distance in each leg:

`\begin{gathered} d=9+30 \\ d=39 \end{gathered}`

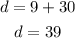
Therefore, the boat traveled 39 m