Answer:
Approximately
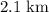 , assuming that
, assuming that
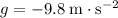 .
.
Step-by-step explanation:
Let
 denote the time required for the package to reach the ground. Let
denote the time required for the package to reach the ground. Let
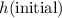 and
and
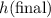 denote the initial and final height of this package.
denote the initial and final height of this package.
 .
.
For this package:
- Initial height:
 .
. - Final height:
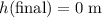 (the package would be on the ground.)
(the package would be on the ground.)
Solve for
 , the time required for the package to reach the ground after being released.
, the time required for the package to reach the ground after being released.
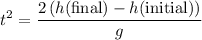 .
.
 .
.
Assume that the air resistance on this package is negligible. The horizontal ("forward") velocity of this package would be constant (supposedly at
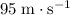 .) From calculations above, the package would travel forward at that speed for about
.) From calculations above, the package would travel forward at that speed for about
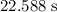 . That corresponds to approximately:
. That corresponds to approximately:
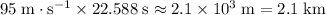 .
.
Hence, the package would land approximately
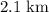 in front of where the plane released the package.
in front of where the plane released the package.