Question

Which statement is true about the polynomial

5s6t2 + 6st9 _ 8s6t2 _ 6t7 after it has been fully simplified?

It has 3 terms and a degree of 9.
It has 3 terms and a degree of 10.
It has 4 terms and a degree of 9.
It has 4 terms and a degree of 10.

Answer 1

It has 3 terms and a degree of 10

Step-by-step explanation:

The given expression is:

`5s^(6) t^(2) + 6st^(9) - 8s^(6) t^(2) - 6t^(7)`

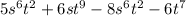
We will start by simplifying the expression by gathering like terms. Remember that like terms are terms having the same degree for all variables they contain.

Now, in the given expression, we can note that:

`5s^(6) t^(2)` and
`-8s^(6) t^(2)` are like terms. This is because, in both terms, the degree of "s" is 6 and the degree of "t" is 2.

This means that we can add these two terms. This will give us:

`-3s^(6) t^(2) + 6st^(9) - 6t^(7)`

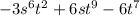
Now, as we can note, no further simplification is possible as there are no like terms.

Now, it's obvious that the expression we reached has 3 terms:

`-3s^(6) t^(2) , 6st^(9) and - 6t^(7)`

Finally, let's get the degree of the expression.

The degree of the expression is defined by the largest degree of its terms. To get the degree of each term, we simply add the powers of the variables as follows:

`-3s^(6) t^(2)` has a deree of 6+2 = 8

`6st^(9)` has a deree of 1+9 = 10

`-6t^(7)` has a deree of 7

As we can note, the highest degree is 10. This means that our expression is of degree 10

From the above, we can conclude that:

After simplification, the expression will have 3 teams and a degree of 10

Hope this helps :)

Answer 2

Consider the polynomial
`5s^6t^2 + 6st^9 - 8s^6t^2 - 6t^7`.

You can see that there are two terms
`5s^6t^2` and
`- 8s^6t^2` that have the same degree at s and t variables. So you can add these two terms:

`5s^6t^2- 8s^6t^2=s^6t^2(5-8)=-3s^6t^2.`

Then the polynomial
`5s^6t^2 + 6st^9 - 8s^6t^2 - 6t^7` is simplified to

`6st^9 - 3s^6t^2 - 6t^7.`

This polynomial has three terms
`6st^9,\ - 3s^6t^2\ \text{ and } - 6t^7.`

Determine the degree of each of these terms:

1. 
   `6st^9` has degree 1+9=10;
2. 
   `- 3s^6t^2` has degree 6+2=8;
3. 
   `- 6t^7` has degree 7.

The maximal degree is 10, thus the polynomial has 3 terms and a degree of 10.

Answer: correct choice is B.