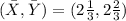Question

A uniform piece of sheet steel is shaped as in the figure below. (Both axes are marked in increments of 2). Compute the x and y coordinates of the center of mass of the piece.

Answer 1

`(\bar{X},\bar{Y})=(2(1)/(3),2(2)/(3))`

Step-by-step explanation:

Since the given sheet is of steel hence it has a homogeneous density, each piece of square measurement according to the graph will have equal mass.

For X coordinate of center of mass:

`\bar{X}=(m_1.x_1+m_2.x_2+m_3.x_3+m_4.x_4+m_5.x_5+m_6.x_6)/(m_1+m_2+m_3+m_4+m_5+m_6)`

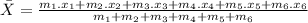
where:

`x_1,x_2,x_3,x_4,x_5,x_6` are the respective geometric abscissa of square pieces.

Since,

Respective masses of the square pieces

`m_1=m_2=m_3=m_4=m_5=m_6=m\,(let)`

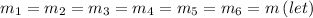
So,

`\bar{X}=m* ((x_1+x_2+x_3+x_4+x_5+x_6))/(6m)`

`\bar{X}= ((3+1+1+1+3+5))/(6)`

`\bar{X}=2(1)/(3)`

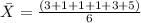
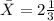
For Y coordinate of center of mass:

`\bar{Y}=(m_1.y_1+m_2.y_2+m_3.y_3+m_4.y_4+m_5.y_5+m_6.y_6)/(m_1+m_2+m_3+m_4+m_5+m_6)`

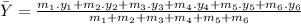
where:

`y_1,y_2,y_3,y_4,y_5,y_6` are the respective geometric ordinates of square pieces.

Since,

Respective masses of the square pieces

`m_1=m_2=m_3=m_4=m_5=m_6=m\,(let)`

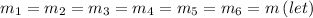
So,

`\bar{Y}=m* ((y_1+y_2+y_3+y_4+y_5+y_6))/(6m)`

`\bar{Y}= ((5+5+3+1+1+1))/(6)`

`\bar{Y}=2(2)/(3)`

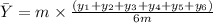
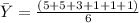
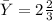
∴Center of mass of the given figure is:

`(\bar{X},\bar{Y})=(2(1)/(3),2(2)/(3))`