Question

The board of directors of a company knows that the probability that the carbon emission from the companyÍs manufacturing unit is exceeding the permissible level is 35%. A consultant is hired to use a carbon footprint calculator to test for the emission level. The accuracy of this test is said to be 85%.

You have this additional information: the test reported that the carbon emission from the manufacturing unit is well within the permissible level. What is the probability that the emission is within the permissible level, given the outcome of the test?

Answer 1

The probability that the emission is within the permissible level, given the outcome of the test is 0.9132

Explanation:

For this exercise we need to define certain events:

NP: Exceeding the permissible level of carbon emission

P: Not exceed the permissible level of carbon emission

NPT: the test said that the company exceed the permissible level

PT: the test said that the company don't exceed the permissible level

Additionally the accuracy is the probability that the test say something and that is according with reality.

From the information we have 4 possible cases with their respective probabilities:

1. the company exceed the permissible level and the test said the same: this can be calculate as the multiplication of the probability that the company exceed the permissible level (35%) and the accuracy of the test (85%), so:

P(NP y NPT)=0.35*0.85= 0.2975

2. the company exceed the permissible level and the test said the opposite: this can be calculate as the multiplication of the probability that the company exceed the permissible level (35%) and the complement of the accuracy of the test (15%), so:

P(NP y PT)=0.35*0.15= 0.0525

3. the company doesn't exceed the permissible level and the test said the same: this can be calculate as the multiplication of the probability that the company doesn't exceed the permissible level (65%) and the accuracy of the test (85%), so:

P(P y PT)=0.65*0.85= 0.5525

4. the company doesn't exceed the permissible level and the test said the opposite: this can be calculate as the multiplication of the probability that the company doesn't exceed the permissible level (65%) and the complement of the accuracy of the test (15%), so:

P(P y NPT)=0.65*0.15= 0.0975

Then the probability that the emission is within the permissible level, given the outcome of the test can be written and calculate as:

`P(P/PT)=(P(P y PT))/(P(PT))`

the probability of PT can be calculate as the sum of every possible case that involve PT, so:

P(PT)=P(NP y PT) + P(P y PT)

P(PT)=0.0525+0.5525 = 0.605

therefore replacing values on the initial equation we get:

`P(P/PT)=(0.5525)/(0.605)`

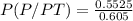
P(P/PT)=0.9132

Finally, The probability that the emission is within the permissible level, given the outcome of the test is 0.9132

Answer 2

I think you forgot to give the options along with the question. I am answering the question based on my knowledge and research.
Probability that the emission is within the permissible level = 0.65 * 0.85
= 0.5525

From the above deduction, it can be concluded that the probability that the emission is within the permissible level is 0.5525. I hope that this is the answer that has actually come to your desired help.