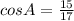Answer:
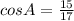
Explanation:
Since, In a right triangle,
If
 is an acute angle,
is an acute angle,
Then,
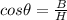
Where, B is the adjacent side of
 ( Except hypotenuse ),
( Except hypotenuse ),
And, H is the hypotenuse of the triangle,
Here,
 ,
,
Hypotenuse of the triangle, H = 17 cm,
While, the adjacent side of angle A, B = 15 cm,
Thus,