Question

A stretched spring has 5184 J of elastic potential energy and a spring constant of 16,200 N/m. What is the displacement of the spring?

0.57 m
0.64 m
0.80 m
1.25 m

Answer 1

Hello!

A stretched spring has 5184 J of elastic potential energy and a spring constant of 16,200 N/m. What is the displacement of the spring?

0.57 m

0.64 m

0.80 m

1.25 m

Data:

`E_(pe)\:(elastic\:potential\:energy) = 5184\:J`

`K\:(constant) = 16200\:N/m`

`x\:(displacement) =\:?`

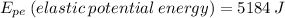
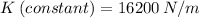
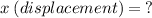
For a spring (or an elastic), the elastic potential energy is calculated by the following expression:

`E_(pe) = (k*x^2)/(2)`

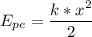
Where k represents the elastic constant of the spring (or elastic) and x the deformation or displacement suffered by the spring.

Solving:

`E_(pe) = (k*x^2)/(2)`

`5184 = (16200*x^2)/(2)`

`5184*2 = 16200*x^2`

`10368 = 16200\:x^2`

`16200\:x^2 = 10368`

`x^(2) = (10368)/(16200)`

`x^(2) = 0.64`

`x = √(0.64)`

`\boxed{\boxed{x = 0.8\:m}}\end{array}}\qquad\checkmark`

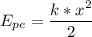
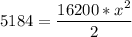
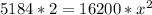
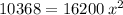
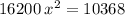
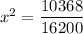
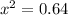
Answer:

The displacement of the spring = 0.8 m (or 0.80 m)

_________________________________________

I Hope this helps, greetings ... Dexteright02! =)

Answer 2

Simply use the equation E = 0.5kx^2. Here E is the elastic potential energy stored in the spring, k is the spring constant and x is the extension. We are solving for extension:

E = 0.5kx^2
x = sqrt(2E/k) = sqrt((2*5184)/16200) = 0.80m

I hope this helps you :)