Given:
w varies jointly as x and y.
w=10 when x=2 and y=1.
To find:
The value of w when x=4 and y=2.
Solution:
w varies jointly as x and y.
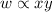
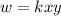 ...(i)
...(i)
Where, k is the constant of proportionality.
w=10 when x=2 and y=1.
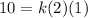
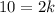
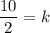
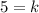
The value of k is 5.
Putting k=5 in (i), we get
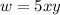
To find the value of w when x=4 and y=2. Put x=4 and y=2.
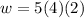
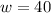
Therefore, the value of w is 40 when x=4 and y=2.