Question

The height (h) in feet of a projectile shot straight up from a cliff 260 feet tall (t) seconds after itbegins is given by h = -16t2 + 48t + 260. When will it be 100 feet above the canyon floor?

Answer 1

To solve the exercise, it is helpful to draw the situation described in the statement:

Since we have the height after which the projectile will have to be at t seconds, then we replace h = 100 in the given equation and solve for t:

`\begin{gathered} h=100 \\ h=-16t^2+48t+260 \\ 100=-16t^2+48t+260 \\ \text{ Subtract 100 from both sides of the equation} \\ 100-100=-16t^2+48t+260-100 \\ 0=-16t^2+48t+160 \end{gathered}`

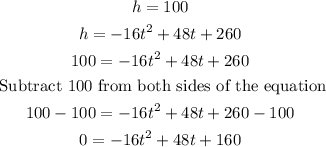
To solve the quadratic equation above, we can use the quadratic formula:

`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a}\Rightarrow\text{ Quadratic formula} \\ \text{For }ax^2+bx+c=0\Rightarrow\text{ Quadratic equation in standard form} \end{gathered}`

In this case, we have:

`\begin{gathered} a=-16 \\ b=48 \\ c=160 \end{gathered}`
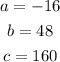
`\begin{gathered} x=\frac{-b\pm\sqrt[]{b^2-4ac}}{2a} \\ \text{ In this case, x = t} \\ t=\frac{-48\pm\sqrt[]{(48)^2-4(-16)(160)}}{2(-16)} \\ t=\frac{-48\pm\sqrt[]{2304+4(16)(160)}}{-32} \\ t=\frac{-48\pm\sqrt[]{2304+10240}}{-32} \\ t=(-48\pm112)/(-32) \end{gathered}`

There are two possible solutions for the quadratic equation:

`\begin{gathered} t_1=(-48+112)/(-32) \\ t_1=(64)/(-32) \\ t_1=-2 \end{gathered}`
`\begin{gathered} t_2=(-48-112)/(-32) \\ t_2=(-160)/(-32) \\ t_2=5 \end{gathered}`

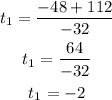
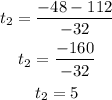
Since it makes no sense to say that time is negative, then the solution to the equation is t = 5.

Therefore, the projectile will be 100 feet above the canyon floor when 5 seconds have passed after its shot.