Question

The hydrogen atom can absorb light of wavelength 1094 nm. Find the initial and final values of n associated with this absorption.

**I know this has something to do with rydberg's equation, however I'm not exactly sure how to go about this.

Answer 1

Rydberg equation is


`(1)/(wavelength)= R( (1)/( n_(1)^(2) )-(1)/( n_(2)^(2) ))`

R is the Rydberg constant which is equal to 1.096776 x 10^7 m^-1. Wavelength is 1.094 x 10^-6 m.

So the equation becomes,


`(1)/(1.094 \ x \ 10^(-6) )=1.096776 \ x \ 10^(7)( (1)/( n_(1)^(2) )-(1)/( n_(2)^(2) ))`

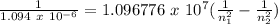
This is trial and error. Our basis should be: n2>n1 and both are whole numbers. According to quantum theory, electrons jump in discrete energies, so there is no in-between. Energy levels must be in a specific quantum number. Then, in order to absorb light, the photon must be able to go to a higher energy level.

If n1 = 1, n2 = 1.04
n1 = 2, n2 = 2.45
n1 = 3, n2 = 6

Hence, n1 = 3 and n2 = 6.