Question

From the triangle below, if AD = 3 and CD = 12, find the length of side BD.

Answer 1

6

Explanation:

Answer 2

step 1

In the right triangle ABD

Applying the Pythagorean Theorem

`\begin{gathered} AB^2=AD^2+BD^2 \\ AB^2=3^2+BD^2 \\ AB^2=9+BD^2\text{ ----> equation 1} \end{gathered}`

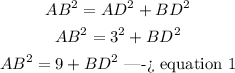
step 2

In the right triangle BCD

Applying the Pythagorean Theorem

`\begin{gathered} BC^2=DC^2+BD^2 \\ BC^2=12^2+BD^2 \\ BC^2=144+BD^2\text{ ----> equation 2} \end{gathered}`

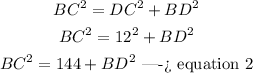
step 3

In the right triangle ABC

Applying the Pythagorean Theorem

`\begin{gathered} AC^2=AB^2+BC^2 \\ 15^2=AB^2+BC^2 \\ 225=AB^2+BC^2\text{ ----> equation 3} \end{gathered}`

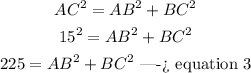
substitute equation 1 and equation 2 in equation 3

`225=(9+BD^2)+(144+BD^2)`

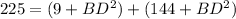
Solve for BD

`\begin{gathered} \begin{equation*} 225=(9+BD^2)+(144+BD^2) \end{equation*} \\ 225-153=2BD^2 \\ BD^2=(72)/(2) \\ \\ BD^2=36 \\ BD=6 \end{gathered}`

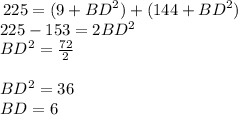
The answer is the option C