Answer:
The expression which will result in difference of two squares is:
(–7x + 4)·(–7x – 4)
Explanation:
We know that the formula of the type:
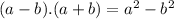
i.e. it is a difference of two square quantities. (a^2 and b^2)
Hence the option which satisfies the following expression is:
(-7x + 4)·(-7x-4)
since,
here
 and
and
 and
and
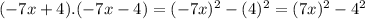
so the expression is a difference of two square quantities:
 and
and
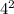
Hence, the correct answer is:
(-7x + 4)·(-7x-4)