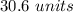see the attached figure to better understand the problem
Let
x------> the length side of a rectangle
y-------> the width side of a rectangle
we know that
the perimeter of a rectangle is equal to the formula

In this problem

Step 1
Find the distance AB
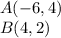
we know that
the distance's formula between two points is equal to

substitute the values
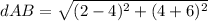
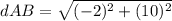
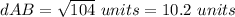
Step 2
Find the distance BC
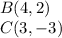
we know that
the distance's formula between two points is equal to

substitute the values
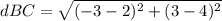

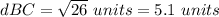
Step 3
Find the perimeter
we know that
the perimeter of a rectangle is equal to the formula

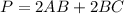
substitute the values of the distance in the formula

therefore
the answer is
The perimeter of the rectangle is equal to