Question

A geometric sequence has terms a3 = 2 and a9 = 128. Find the explicit formula for this sequence.

Answer 1

we know that

the explicit formula in a geometric sequence is

`a_n=a_1\cdot(r)^((n-1))`

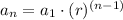
In this problem

we have that

a3=2

a9=128

substitute in the expression above

`\begin{gathered} a_3=a_1\cdot(r)^((3-1)) \\ 2=a_1\cdot r^2 \end{gathered}`

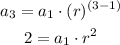
and

`\begin{gathered} a_9=a_1\cdot(r)^((9-1)) \\ 128=a_1\cdot r^8 \end{gathered}`

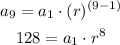
Divide both expressions

128=a1*(r^8)

2=a1*(r^2)

----------------

128/2=r^8/r^2

64=r^6

r=2

Find out the value of a1

2=a1*(r^2)

2=a1*(2^2)------> 2=a1*4

a1=1/2

therefore

a1=1/2 and r=2

the explicit formula is equal to

`a_n=(1)/(2)\cdot(2)^((n-1))`

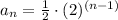
the answer is option C