we know that
the explicit formula in a geometric sequence is
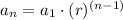
In this problem
we have that
a3=2
a9=128
substitute in the expression above
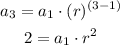
and
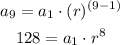
Divide both expressions
128=a1*(r^8)
2=a1*(r^2)
----------------
128/2=r^8/r^2
64=r^6
r=2
Find out the value of a1
2=a1*(r^2)
2=a1*(2^2)------> 2=a1*4
a1=1/2
therefore
a1=1/2 and r=2
the explicit formula is equal to
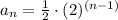
the answer is option C