Question

3.Match each function notation with the transformation that has been performed:A._______ B._______ C._______ D._______ E._______ F._______A. f(x-3)B. f(-x)C. 2f(x)D. -f(x)F. f(x)+2G. f(3x)U. Horizontal translationV. Vertical translationW. Horizontal compressionX. Vertical stretchY. X-axis reflectionZ. Y-axis reflection

Answer 1

So,

First, remember that:

Given a function f(x). If we make the following changes to it (where c is a number), they will represent:

1. Horizontal translation.

`f(x\pm c)`

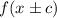
The expression above represents a horizontal translation.

So, if we have f (x - 3) this is a horizontal translation 3 units to the right.

If the sign is positive, the graph moves to the left and if it's negative, it moves to the right.

2. Vertical translation:

`f(x)\pm c`

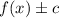
The expression above represents a vertical translation.

So, if we have f(x) + 2, this change represents a vertical translation 2 units up.

If the sign is positive, the graph moves c units up, and if it is negative, the graph moves c units down.

3. X-axis reflection.

`-f(x)`

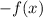
The expression above represents a X-axis reflection.

So, given -f(x), that's a reflection over the x-axis.

4. y-axis reflection.

`f(-x)`

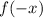
The expression above represents a y-axis reflection.

So, given f(-x), that's a reflection over the y-axis.

5. Horizontal compression:

`f(cx)`

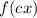
If |c| is greater than 1, this is a horizontal compression.

If |c| is between 0 and 1, this is a horizontal stretch.

In our problem, we are given f(3x), and, as 3 is greater than 1, we have a horizontal compression.

6. Vertical stretch:

`cf(x)`

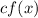
If |c| is greater than 1, this is a horizontal compression.

If |c| is between 0 and 1, this is a horizontal stretch.