So,
First, remember that:
Given a function f(x). If we make the following changes to it (where c is a number), they will represent:
1. Horizontal translation.
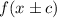
The expression above represents a horizontal translation.
So, if we have f (x - 3) this is a horizontal translation 3 units to the right.
If the sign is positive, the graph moves to the left and if it's negative, it moves to the right.
2. Vertical translation:
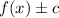
The expression above represents a vertical translation.
So, if we have f(x) + 2, this change represents a vertical translation 2 units up.
If the sign is positive, the graph moves c units up, and if it is negative, the graph moves c units down.
3. X-axis reflection.
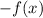
The expression above represents a X-axis reflection.
So, given -f(x), that's a reflection over the x-axis.
4. y-axis reflection.
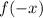
The expression above represents a y-axis reflection.
So, given f(-x), that's a reflection over the y-axis.
5. Horizontal compression:
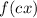
If |c| is greater than 1, this is a horizontal compression.
If |c| is between 0 and 1, this is a horizontal stretch.
In our problem, we are given f(3x), and, as 3 is greater than 1, we have a horizontal compression.
6. Vertical stretch:
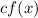
If |c| is greater than 1, this is a horizontal compression.
If |c| is between 0 and 1, this is a horizontal stretch.