Question

If y = 7x – 5, which of the following sets represents possible inputs and outputs of the function, represented as ordered pairs? (5 points) {(–5, 0), (9, 2), (–26, –3)} {(2, 7), (1, 6), (3, 13)} {(0, –5), (2, 9), (–3, –26)} {(1, 3), (6, 18), (8, 15)}

Answer 1

The third set, (0, -5) (2,9) (-3,-26)

Answer 2

The third set is the correct option.

Explanation:

We have the following function :

`y=7x-5`

We can also write it as

`f(x)=7x-5`

• This means that the function ''f'' depends of the variable x.
• The possible inputs of the function are the values that the "x" can assume.

Now, given a possible ''x'', if we replace it in the expression of f(x) the result will be a possible output that matches that input.

For example, If
`x=0` ⇒

`y=7.(0)-5=-5`

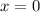If x = 0 ⇒ y = -5

The pair
`(x,y)=(0,-5)` is a possible input-output pair.

In this exercise we have 4 sets. In order to find a set of possible input-output pairs, we need to replace them in the equation of the function.

• The first set is {(-5,0),(9,2),(-26,-3)}

If we replace each pair in the function :

`0=7(-5)-5=-40`

`0=-40`

The pair (-5,0) is not a possible pair of input-output. Therefore,we can't say that all the set is a possible pair of input-output for the function.

• The second set is {(2,7),(1,6),(3,13)}

Replacing each pair in the function :

`7=7.(2)-5=9`

`7=9`

Therefore the pair (2,7) is not a possible pair of input-output for the function and we can't say that all the set is a possible input-output set for the function.

• The third set is {(0,-5),(2,9),(-3,-26)}

If we replace each pair in the function

`-5=7.(0)-5`

`-5=-5`

The second pair

`9=7.(2)-5=9`

`9=9`

The last pair

`-26=7.(-3)-5`

`-26=-26`

All pairs match the function. Therefore the third set of pairs is a possible pair of input-output for the function.

• The last set {(1,3),(6,18),(8,15)}

If we replace in the function each pair

`3=7(1)-5=2`

`3=2`

The pair (1,3) is not a possible input-output pair for the function. Therefore, we can't say that all the set is a possible input-output set of pairs for the function.

The set {(0,-5),(2,9),(-3,-26)} represents a possible set of input-output pairs for the function.