Question

Using the interquartile range which of the following are outliner select all correct answers

Answer 1

We can see a five-number summary for a set of data, and this is given as follows:

Where:

• Min = 5 is the minimum value of the set of data

,

• Q1 = 84, represents the First Quartile of the data, that is, the number that tells us that 25% of the data is below this number, and 75% of the data is above it.

,

• Median = 89, represents the value for which 50% of the values are below and above this number.

,

• Q3 = 98 represents the Third Quartile, and this number tells us that 75% of the observations are below this number, and 25% of the observations are above this number.

,

• Max = 99 is the maximum value observed in that set of data.

And we have to find outliers or values that are unusually large or small with respect to the given set of data.

1. To find those outliers, first, we have to find the interquartile range (IQR) as follows:

`IQR=Q3-Q1`

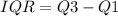
Then we have:

`\begin{gathered} IQR=98-84=14 \\ \\ IQR=14 \end{gathered}`

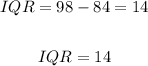
Therefore, the IQR = 14.

2. Now, we have that the outliers can be found using the following formulas:

`\begin{gathered} \text{ Outliers are found for values:} \\ \\ \\ \text{ Greater than }Q3+(1.5IQR) \\ \\ \text{ Less than }Q1-(1.5IQR) \end{gathered}`

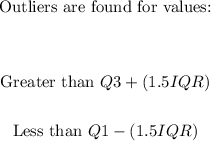
This is known as the Boxplot rule.

3. Now we can find the outliers as follows:

`\begin{gathered} Q3+1.5IQR=98+1.5(14)=98+21=119 \\ \\ \text{ Therefore if we have that any value greater than 119 will be an outlier.} \end{gathered}`

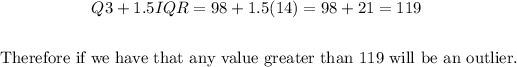
And also we have:

`\begin{gathered} Q1-1.5IQR=84-1.5(14)=84-21=63 \\ \\ \text{ Therefore if we have a value less than 63 will be an outlier.} \end{gathered}`

4. Now, we have:

• If we have from the data a value greater than 119, it will be an outlier. From the given data, we have that there is no value greater than 119.

• If we have from the data a value less than 63, it will be an outlier. From the data set, we have that 42 and 6 are less than 63. Therefore, they are outliers.

Therefore, in summary, we can say that 6 and 42 are outliers (the first and the second options).