If the x coordinate of the foci of an ellipse is the same on both foci, we call this an ellipse with a major axis parallel to the y-axis. The equation of these ellipses is:
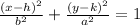
Where:
The length of the major axis is 2a
The coordinates of the foci are: (h, k ± c), where c² = a² - b²
In this case, we can see that the x-coordinate on both foci is the same: 4. Thus, this is an ellipse with its major axis parallel to the y-axis, with a major axis length of 18, and the coordinates of the foci are (4, 7) and (4, 11)
From this, we can find a:
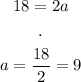
We can also see that h = 4. We need to find k and b.
We know:
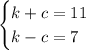
We can add these equations:

And solve for k:
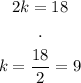
Now that we know k = 9, we can find c:

And finally, use the formula to find b:
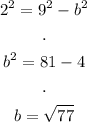
We have all the needed values:

We can write:
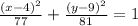
The correct answer is option A.