Question

A pizza shop is running a special on 4 topping pizzas there are 15 toppings total to choose from each topping can be chosen at most once how many different 4 topping pizzas could be chosen

Answer 1

1365 different pizzas

Step-by-step explanation:

The number of ways to select 4 toppings from the 15 toppings in total can be calculated using combinations.

So, we will use the following equation

`nCx=(n!)/(x!(n-x)!)`

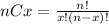
Where n = 15 and x = 4. So, we get

`\begin{gathered} 15C4=(15!)/(4!(15-4)!) \\ \\ 15C4=(15!)/(4!(11!)) \\ \\ 15C4=(15\cdot14\cdot13\cdot12\cdot11!)/(4\cdot3\cdot2\cdot1\cdot11!) \\ \\ 15C4=1365 \end{gathered}`

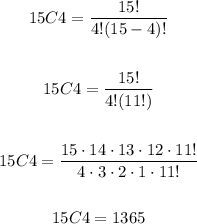
Therefore, there are 1365 different 4 topping pizzas.