Answer:
Triangle MNP is Isosceles.
Step-by-step explanation:
If triangle MNP has vertices at M(-5,-7), N(7,-2) and P(2,10)
To determine if it is Isosceles or not, we have to find the side lengths using the distance formula.
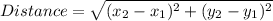
Therefore:
![\begin{gathered} MN=\sqrt[]{(-5-7)^2+(-7-(-2))^2} \\ =\sqrt[]{(-12)^2+(-7+2)^2} \\ =\sqrt[]{(-12)^2+(-5)^2} \\ =\sqrt[]{169} \\ =13\text{ units} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/p89idaqx9jjt3ae0zj9f.png)
Similarly:
![\begin{gathered} MP=\sqrt[]{(-5-2)^2+(-7-10)^2} \\ =\sqrt[]{(-7)^2+(-17)^2} \\ =\sqrt[]{338^{}} \\ =13\sqrt[]{2}\text{ units} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/5re2z584eniqhbmx74xv.png)
Finally:
![\begin{gathered} NP=\sqrt[]{(7-2)^2+(-2-10)^2} \\ =\sqrt[]{(5)^2+(-12)^2} \\ =\sqrt[]{169^{}} \\ =13\text{ units} \end{gathered}](https://img.qammunity.org/qa-images/2023/formulas/mathematics/college/gqg4ig202w2v1bc46esu.png)
We see that:
MN=NP=13 Units
Since two sides are equal in length, triangle MNP is Isosceles.