Question

Chain Rule : Calculus problem

Find the derivative of
f(x) = sqrt[cos(5x)]
The answer is supposedly -5sin(5x)/2sqrtcos(5x)
How does one arrive at this answer?

Answer 1

`\displaystyle f'(x) = (-5sin(5x))/(2√(cos(5x)))`

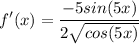
General Formulas and Concepts:

Algebra I

Functions

• Function Notation

Exponential Rule [Rewrite]:
`\displaystyle b^(-m) = (1)/(b^m)`

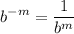
Exponential Rule [Root Rewrite]:
`\displaystyle \sqrt[n]{x} = x^{(1)/(n)}`

Calculus

Differentiation

• Derivatives
• Derivative Notation

Derivative Property [Multiplied Constant]:
`\displaystyle (d)/(dx) [cf(x)] = c \cdot f'(x)`

Basic Power Rule:

1. f(x) = cxⁿ
2. f’(x) = c·nxⁿ⁻¹

Derivative Rule [Chain Rule]:
`\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)`

Trig Derivatives

Explanation:

Step 1: Define

Identify

`\displaystyle f(x) = √(cos(5x))`

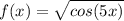
Step 2: Differentiate

1. Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle f(x) = [cos(5x)]^\bigg{(1)/(2)}`
2. Derivative Rule [Chain Rule]:
   `\displaystyle f'(x) = (d)/(dx) \bigg[ [cos(5x)]^\bigg{(1)/(2)} \bigg] \cdot (d)/(dx)[cos(5x)] \cdot (d)/(dx)[5x]`
3. Rewrite [Derivative Property - Multiplied Constant]:
   `\displaystyle f'(x) = (d)/(dx) \bigg[ [cos(5x)]^\bigg{(1)/(2)} \bigg] \cdot (d)/(dx)[cos(5x)] \cdot 5(d)/(dx)[x]`
4. Basic Power Rule:
   `\displaystyle f'(x) = (1)/(2)[cos(5x)]^\bigg{(1)/(2) - 1} \cdot (d)/(dx)[cos(5x)] \cdot 5x^(1 - 1)`
5. Simplify:
   `\displaystyle f'(x) = (5)/(2)[cos(5x)]^\bigg{(-1)/(2)} \cdot (d)/(dx)[cos(5x)]`
6. Trig Derivative:
   `\displaystyle f'(x) = (5)/(2)[cos(5x)]^\bigg{(-1)/(2)} \cdot -sin(5x)`
7. Simplify:
   `\displaystyle f'(x) = (-5sin(5x))/(2)[cos(5x)]^\bigg{(-1)/(2)}`
8. Rewrite [Exponential Rule - Rewrite]:
   `\displaystyle f'(x) = \frac{-5sin(5x)}{2[cos(5x)]^\bigg{(1)/(2)}}`
9. Rewrite [Exponential Rule - Root Rewrite]:
   `\displaystyle f'(x) = (-5sin(5x))/(2√(cos(5x)))`

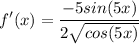
Topic: AP Calculus AB/BC (Calculus I/I + II)

Unit: Derivatives

Book: College Calculus 10e