Answer:
 ≈ 4.0233...
≈ 4.0233...
Explanation:
First we identify the function:
![f(x)=\sqrt[3]{x^(2) }](https://img.qammunity.org/2017/formulas/mathematics/college/5teretwvow3o69v03z9ovpgzb59t67phh7.png)
then we take the firts derivative:
![f(x)=\frac{2}{3\sqrt[3]{x}}](https://img.qammunity.org/2017/formulas/mathematics/college/ohanw15u8xq2t85gzpn7yyl7xavrdaduyp.png)
Then we take a starting point a=8, so the function has the value:
![f(8)=\sqrt[3]{8^(2) }=4](https://img.qammunity.org/2017/formulas/mathematics/college/boq9ncvdbvmywn7osw6ob7i28x4w017lad.png)
and the first derivative has the value:
![f(8)=\frac{2}{3\sqrt[3]{8}}=(1)/(3)](https://img.qammunity.org/2017/formulas/mathematics/college/wjeg9cq2q6pam3guub9hshx79ytjic4pyr.png)
Then consider the folowing relation:
f(x) ≈ f(a) + f'(a) (Δx); where Δx = x-a = 8.07-8 = 0.07
Finally we replace the values and find:
 ≈ 4 +(
≈ 4 +(
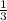 * 0.07)
* 0.07)
 ≈ 4.0233...
≈ 4.0233...