Question

Directions in pic. Please graph and fill in the blanks

Answer 1

From the present question, we can plot the following graph

From the presented equation:

`f(x)=3^(x-2)-7`

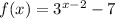
We can see that there is no restriction to the value of x you can use in this equation. It can be evaluated to any given number because the exponential function has as domain all the real numbers. From this, the presented equation also has as domain all the real numbers.

For the range, it is better to solve the other question before finding it.

Let's calculate the limits:

For x going to the positive infinity, the value of x - 2 will go to the positive infinity also, and the exponent of x-2 goes to the same value. From this, we conclude:

`x\to\infty\Rightarrow f(x)\to\infty`

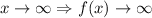
Using the same idea, if x goes to the negative infinity, x-2 goes also to negative infinity and the exponential of negative infinity goes to zero, it is:

`x\to-\infty\Rightarrow f(x)=-7`

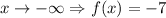
From these two answers, we also conclude that the Range of the equation is (-7, +∞)

the y-intercept is the value where x = 0. For this, we just need to substitute the value in the equation, as follows:

`\begin{gathered} f(x=0)=3^(0-2)-7 \\ f(0)=3^(-2)-7=(1)/(9)-7=-(62)/(9) \\ y=-(62)/(9) \end{gathered}`

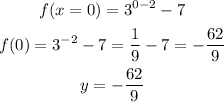
The asymptote is calculated from the limits to + infinity and - infinity, and from those calculated above we can conclude the only asymptote is:

`y=-7`

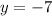
From this, we conclude:

Domains = all the real numbers

Range = (-7, +∞)

Behavior:

x -> +∞ ⇒ f(x) -> +∞

x -> -∞ ⇒ f(x) -> -7

y-intercept = - 62 / 9

Asymptote: y = -7