Question

I don’t know how to do this can you help me with it?

Answer 1

We have a company with a profit, at year 2007, of $4 million.

This profit increases by 14% per year.

We have to find the profit expected for 2011.

This is a case that can be modeled by an exponential growth equation:

`P(t)=a\cdot b^t`

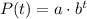
where t represents the number of years after 2007.

Then, we now have to find the parameters "a" and "b".

We can find "a" using the fact that P(0), that is the profit in 2007, was 4 million.

Then, we can write:

`\begin{gathered} P(0)=4 \\ a\cdot b^0=4 \\ a\cdot1=4 \\ a=4 \end{gathered}`

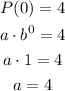
Now, we can relate two consecutive years to find "b".

We know that the profit of one year P(t) is equal to 14% more than the profit of the previous year P(t-1). We then can write it as:

`\begin{gathered} P(t)=P(t-1)+0.14-P(t-1) \\ P(t)=1.14\cdot P(t-1) \\ (P(t))/(P(t-1))=1.14 \\ (a\cdot b^t)/(a\cdot b^(t-1))=1.14 \\ b^(t-(t-1))=1.14 \\ b^1=1.14 \\ b=1.14 \end{gathered}`

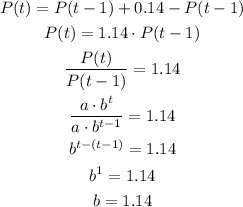
Now, we know that a = 4 and b = 1.14 and the model becomes:

`P(t)=4\cdot1.14^t`

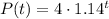
We have to find the profit for 2011, which correspond to a value of t that is:

`t=2011-2007=4`

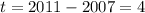
We can use the model for t = 4 to calculate the profit in 2011:

`\begin{gathered} P(4)=4\cdot1.14^4 \\ P(4)\approx4\cdot1.689 \\ P(4)\approx6.756 \\ P(4)\approx6.8 \end{gathered}`

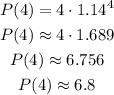
Answer: the profit in 2011 is $6.8 milllion.