Question

Marcus painted one wall of his entryway as an accent wall. The wall is a trapezoid, where the shorter side is 9 feet tall and the longer side is 15 feet tall. The length of the wall is 13 feet. He did not paint the door, which is 7 feet by 2.5 feet. He also did not paint the triangular window, which has a height of 3 feet and a base of 6 feet.What is the area of the wall that Marcus painted?

Answer 1

the Given the geometry of the wall as shown below

The wall takes the shape of a trapezoid.

The unpainted door labeled as A takes the shape of a rectangle.

The unpainted window labeled as B takes the shape of a triangle.

The area of the wall painted by Marcus is evaluated as

`\text{Area of the wall - (area of the unpainted door + area of the unpainted window)}`

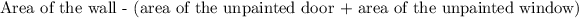
Area of the wall:

Recall that the wall takes the shape of a trapezoid. Thus, the area of a trapezoid is evaluated as

`\begin{gathered} A_(wall)=\text{ }(1)/(2)(a+b)h \\ \text{where} \\ a\text{ and b are the base lengths of the trapezoid} \\ h\text{ is the height of the trapezoid} \end{gathered}`

Thus, the area of the wall becomes

`\begin{gathered} (1)/(2)*(9+15)*13 \\ =(1)/(2)*24*13\text{ = 12}*13 \\ \Rightarrow156\text{ square-f}eet \\ \end{gathered}`

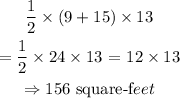
Area of the unpainted door:

Recall that the unpainted door, labeled as A, takes the shape of a rectangle. Hence, the area of a rectangle is evaluated as

`\begin{gathered} A_{\text{rectangle}}=\text{ l }* b \\ \text{where} \\ l\Rightarrow\text{length of the rectangle } \\ b\Rightarrow\text{width of the rectangle } \end{gathered}`

The area of the unpainted door becomes

`\begin{gathered} A_{unpainted\text{ door}}=7*2.5\text{ } \\ \Rightarrow17.5\text{ square-f}eet \end{gathered}`

Area of the unpainted window:

Recall that the unpainted window, labeled as B, takes the shape of a triangle. Thus, the area of a triangle is evaluated as

`\begin{gathered} A_(triangle)\text{ = }(1)/(2)bh \\ \text{where} \\ b\Rightarrow base\text{ length of the triangle} \\ h\Rightarrow height\text{ of the triangle} \end{gathered}`

Thus, the area of the unpainted window becomes

`\begin{gathered} A_{unpainted\text{ window}}=(1)/(2)*3*6 \\ =3*2 \\ \Rightarrow6\text{ square-fe}et \end{gathered}`

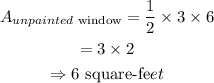
Thus, the area of the painted wall becomes

`\begin{gathered} A_{painted\text{ wall}}\text{ = 156 - (17.5 + 6)} \\ =156\text{ - 23.5} \\ \Rightarrow132.5\text{ square-fe}et \end{gathered}`

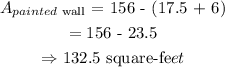
Hence, the area of the wall painted by Marcus is 132.5 square-feet