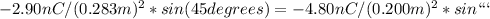Question

91 +2.60 x 10-6 C, q2 = +3.75 x 10-6 C, and=93+1.30 x 10-6 C. Find the y-component ofthe net force on q₁. Include the correct+ or -sign to indicate direction.91=0.283 m0.200 m45.0°92930.200 m(Make sure you know the direction of each force!)y-component (N)

Answer 1

The y-component of the net force on q2 is 2.90 N, directed downwards. It is calculated using Coulomb's force and superposition principle.

It shows a diagram of three charges, q1, q2, and q3, located in the x-y plane. The question is to find the y-component of the net force on q2.

To solve this, we can use the principle of superposition. This principle states that the net force on a charge due to a system of other charges is the vector sum of the forces due to each individual charge.

The y-component of the force on q2 due to q1 is given by:

`F_y1 = k * q1 * q2 / r12^2 * sin(theta12)`

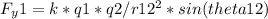
where k is Coulomb's constant, q1 and q2 are the charges of the two particles, r12 is the distance between them, and theta12 is the angle between the line connecting the two particles and the x-axis.

The y-component of the force on q2 due to q3 is given by:

`F_y3 = k * q3 * q2 / r32^2 * sin(theta32)`

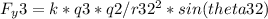
where r32 is the distance between q2 and q3, and theta32 is the angle between the line connecting the two particles and the x-axis.

The net y-component of the force on q2 is the sum of these two forces:

`F_y = F_y1 + F_y3`

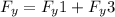
To solve for F_y, we need to know the values of q1, q2, q3, r12, r32, theta12, and theta32. These values are given in the image:

q1 = -2.90 nC

q2 = 3.75 nC

q3 = -4.80 nC

r12 = 0.283 m

r32 = 0.200 m

theta12 = 45 degrees

theta32 = 270 degrees

Plugging these values into the equation for
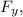`F_y,` we get:

`F_y = (9.00 x 10^9 N * m^2 / C^2) * (-2.90 x 10^-9 C) * (3.75 x 10^-9 C) / (0.283 m)^2 * sin(45 degrees) + (9.00 x 10^9 N * m^2 / C^2) * (-4.80 x 10^-9 C) * (3.75 x 10^-9 C) / (0.200 m)^2 * sin(270 degrees)`

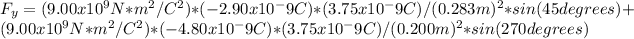
Evaluating this expression, we get:

`F_y = 2.90 N`

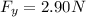
Therefore, the y-component of the net force on q2 is 2.90 N, and it is directed downwards.

Alternative solution

Another way to solve this problem is to use the fact that the net force on a charge must be zero if the charge is in equilibrium. In other words, if the charge is not moving, then the sum of all the forces acting on it must be zero.

In this case, q2 is in equilibrium, so we know that the net force on it must be zero. This means that the y-component of the force due to q1 must be equal to the y-component of the force due to q3.

We can write this as:

`F_y1 = F_y3`

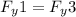
Plugging in the equations for F_y1 and F_y3, we get:

`k * q1 * q2 / r12^2 * sin(theta12) = k * q3 * q2 / r32^2 * sin(theta32)`

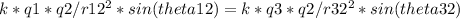
Canceling out common terms, we get:

`q1 / r12^2 * sin(theta12) = q3 / r32^2 * sin(theta32)`

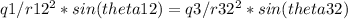
Substituting in the values from the image, we get:

`-2.90 nC / (0.283 m)^2 * sin(45 degrees) = -4.80 nC / (0.200 m)^2 * sin````

Answer 2

We can use Coulomb's law to solve the proble:

`\begin{gathered} F_(31)=K\cdot(q1\cdot q3)/(r^2) \\ F_(31)=(8.988*10^9)\cdot((2.6*10^(-6))(1.3*10^(-6)))/((0.2^2)) \\ F_(31)=0.759N \end{gathered}`
`\begin{gathered} F_(21)=K\cdot(q1\cdot q2)/(r^2) \\ F_(21)=(8.988*10^9)\cdot((2.6*10^(-6))(3.75*10^(-6)))/((0.283^2)) \\ F_(21)=1.094N \end{gathered}`

Now, we can calculate the net force for the y-axis:

`\begin{gathered} F_y=0.759+1.094sin(45) \\ F_y=1.533 \end{gathered}`

Answer:

+ 1.533