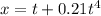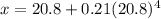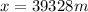Question

A faulty model rocket moves in the xy-plane (the positive y direction is vertically upward). The rocket’s acceleration has components ax(t) = αt2 and ay(t) = β −γt, where α = 2.50 m/s4 , β = 9.00 m/s2 , and γ = 1.40 m/s3 . At t = 0 the rocket is at the origin and has velocity ~v0 = v0x ˆi + v0y ˆj with v0x = 1.00 m/s and v0y = 7.00 m/s. (a) Calculate the velocity and position vectors as functions of time. (b) What is the maximum height reached by the rocket? (c) Sketch the path of the rocket. (d) What is the horizontal displacement of the rocket when it returns to y = 0?

Answer 1

To calculate the velocity and position vectors as functions of time for the faulty model rocket, you need to integrate the given acceleration components. The maximum height reached by the rocket can be found by finding the time at which the vertical velocity is zero. The path of the rocket can be sketched by plotting the position coordinates as a function of time.

Step-by-step explanation:

The velocity and position vectors of the model rocket can be calculated by integrating the given acceleration components. The velocity as a function of time is given by Vx(t) = αt^3/3 + v0x and Vy(t) = βt - γt^2/2 + v0y. The position as a function of time is given by x(t) = αt^4/12 + v0xt + x0 and y(t) = βt^2/2 - γt^3/6 + v0yt + y0, where x0 and y0 are the initial position coordinates.

The maximum height reached by the rocket can be found by finding the time, t, at which Vy(t) = 0. Substituting the values, we can solve for t and then substitute it into the equation for y(t) to find the maximum height.

The path of the rocket can be sketched by plotting the position coordinates (x(t), y(t)) as a function of time. The horizontal displacement of the rocket when it returns to y = 0 can be found by finding the time, t, at which y(t) = 0 and then substituting it into the equation for x(t).

Answer 2

part a)

velocity is given as

`\vec v = ( 1 + (\alpha t^3)/(3))\hat i + (7 + \beta t - (\gamma t^2)/(2))\hat j`

position is given as

`\vec r = (t +( \alpha t^4)/(12))\hat i + (7t +( \beta t^2)/(2) - (\gamma t^3)/(6))\hat j`

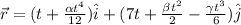
Part b)

maximum height is given as

`y_(max) = 341.4 m`

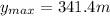
Part c)

Path will be the curved path

Part d)

displacement in x direction will be

`x = 39328 m`

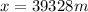
Step-by-step explanation:

`a_x = \alpha t^2`

`a_y  = \beta - \gamma t`

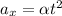
also we know the initial velocity as

`v_0 = 1\hat i + 7 \hat j`

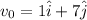
part a)

from acceleration in x direction we can say

`a_x = (dv_x)/(dt) = \alpha t^2`

`\int dv_x = \int \alpha t^2 dt`

`v_x - 1 = (\alpha t^3)/(3)`

`v_x = 1 + (\alpha t^3)/(3)`

`v_x = 1 + 0.83 t^3`

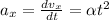
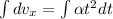
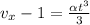
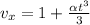
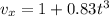
now again integrate both sides

`(dx)/(dt) = (1 + 0.83 t^3)`

`\int dx = \int(1 + 0.83 t^3) dt`

`x = t +( \alpha t^4)/(12)`

`x = t + 0.21 t^4`

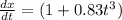
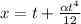
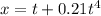
now similarly for y direction

`a_y = (dv_y)/(dt) = \beta - \gamma t`

`\int dv_y = \int (\beta - \gamma t) dt`

`v_y - 7 = \beta t - (\gamma t^2)/(2)`

`v_y = 7 + \beta t - (\gamma t^2)/(2)`

`v_y = 7 + 9 t - 0.70 t^2`

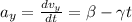
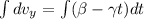
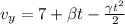
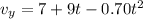
now again integrate both sides

`(dy)/(dt) = (7 + 9t - 0.70t^2)`

`\int dy = \int(7 + 9t - 0.70t^2) dt`

`y = 7t +( \beta t^2)/(2) - (\gamma t^3)/(6)`

`y = 7t + 4.5 t^2 - 0.233 t^3`

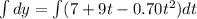
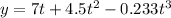
PART B)

For maximum height we know that velocity in y direction must be zero

so we will have

`v_y = 0 = 7 + 9t - 0.70 t^2`

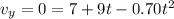
by solving above we have

`t = 13.6 s`

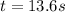
now at this time the height is given as

`y = 7t + 4.5 t^2 - 0.233 t^3`

`y_(max) = 7(13.6) + 4.5(13.6)^2 - 0.233(13.6)^3`

`y_(max) = 341.4 m`

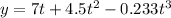
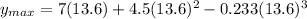
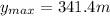
PART C)

path of the rocket will be curved path in xy plane

PART D)

when y = 0 then we have

`y = 0 = 7t + 4.5 t^2 - 0.233 t^3`

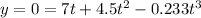
by solving above equation we have

`t = 20.8 s`

now at this time position of X is given as

`x = t + 0.21 t^4`

`x = 20.8 + 0.21(20.8)^4`

`x = 39328 m`