Question

A rectangle has an area of (x2 − 17x 72) square units. since the area of a rectangle is determined using the formula, a = lw, what could be the length and width of the rectangle? length = (x − 8) units and width = (x − 9) units length = (x 9) units and width = (x 8) units length = (x − 6) units and width = (x − 12) units length = (x 12) units and width = (x 6) units

Answer 1

its A

Step-by-step explanation:

Answer 2

Answer: length = (x − 8) units and width = (x − 9) units

Step-by-step explanation:

The area of the rectangle is

`x^2 -17 x + 72`

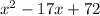
This is a second-order polynome of the form

`ax^2 + bx + c` (1)

with b=-17 and c=72. This type of polynome can be decomposed into the form

`(x+a_1)(x+a_2)`

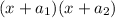
If we rewrite explicitely this last form, we have

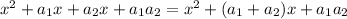`x^2 + a_1 x + a_2 x + a_1 a_2 = x^2 + (a_1 + a_2) x + a_1 a_2` (2)

If we compare (1) with (2), we notice that they are exactly the same form, with:

`a_1 + a_2 = b`

`a_1 a_2 = c`

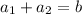
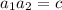
Since we know b=-17 and c=72, we have to find the two numbers
`a_1` and
`a_2` whose sum is -17 and whose product is 72. The two numbers must be both negative (since their product is positive and their sum is negative), so they are:

`a_1 = -8`

`a_2 = -9`

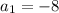
Therefore, the length and the width of the rectangle are

`(x-8)`

`(x-9)`