Answer:
Option A is correct.
the value of the painting ten years after its purchase is, $1,000
Explanation:
Given the function:
 .....[1]
.....[1]
where,
t is the number of years since it was purchased and
v(t) is its value(in dollars) at that time.
We have to find the value of the painting ten years after its purchase.
⇒ t = 10 years
Substitute in [1] we have;
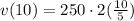
⇒
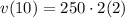
⇒
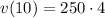
Simplify:
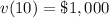
Therefore, the value of the painting ten years after its purchase is, $1,000