Question

A: prove triangle ABC similar to triangle DECB: find BC,DE,and ECC: find the surface areas of the larger cone and the smaller cone in terms of pi. conpare the surface areas using a percentSolve A-C!!

Answer 1

In this case, we'll have to carry out several steps to find the solution.

Step 01:

triangle diagram:

AC = 4

AB = 3

DC = 2

Step 02:

geometry:

similar triangles:

Triangle ABC similar to Triangle DEC:

AA (angle-angle):

∠CAB = ∠ CDE

∠ ABC = ∠ DEC

The triangles are similar

BC:

BC² = AC² + AB²

BC² = (4)² + (3)²

`BC\text{ =}√(16+9)=√(25)=5`

BC = 5

DE:

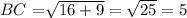
`\begin{gathered} (AC)/(DC)=(AB)/(DE) \\ \\ (4)/(2)=(3)/(DE) \\ \\ 4\text{ * }DE\text{ =3 * 2} \\ \\ DE\text{ = }(6)/(4)=(3)/(2)=1.5 \end{gathered}`

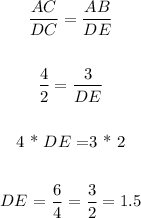
DE = 1.5

EC:

EC² = DC² + DE²

EC² = (2)² + (1.5)²

`EC=√(4+2.25)=√(6.25)=2.5`

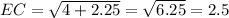
EC = 2.5

That is the full solution.