Question

Given the trinomial x^2-bx-c where both the first and the second signs are negative, the signs of the factors will be:

A. cannot determine
B. both negative
C. both positive
D. one positive and one negative

Answer 1

D

Explanation:

Answer 2

Answer: Option 'D' is correct.

Explanation:

Since we have given that

`x^2-bx-c=0`

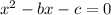
Both the first and second signs are negative,

Let α and β are the roots of the
`x^2-bx-c=0`,

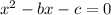then, we know that the relationship between the zeroes and coefficients of quadratic equations:

`\alpha+\beta =(-b)/(a)=b\\\\and\\\\\alpha \beta =(-c)/(a)=-c`

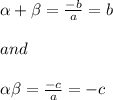
Since the product of roots is positive.

So, the signs of the factors will be one positive and one negative.

Hence, Option 'D' is correct.