ANSWER
17.8 units²
Step-by-step explanation
The area of any triangle is half the product between its base and height. In this case, this is,
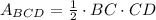
We know that angle B is 36° and its adjacent side, BC, is 7 units long. Since side CD is the opposite side to angle B, we can use the tangent of that angle to find its length,
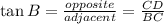
Solving for CD,
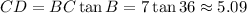
So, the area is,
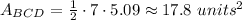
Hence, the area of triangle BCD is 17.8 square units, rounded to the nearest tenth.