Question

What is the area of triangle bcd BC:7 angle b=36

Answer 1

17.8 units²

Step-by-step explanation

The area of any triangle is half the product between its base and height. In this case, this is,

`A_(BCD)=(1)/(2)\cdot BC\cdot CD`

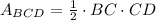
We know that angle B is 36° and its adjacent side, BC, is 7 units long. Since side CD is the opposite side to angle B, we can use the tangent of that angle to find its length,

`\tan B=(opposite)/(adjacent)=(CD)/(BC)`

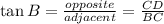
Solving for CD,

`CD=BC\tan B=7\tan36\degree\approx5.09`

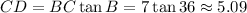
So, the area is,

`A_(BCD)=(1)/(2)\cdot7\cdot5.09\approx17.8\text{ }units^2`

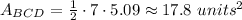
Hence, the area of triangle BCD is 17.8 square units, rounded to the nearest tenth.