For this case we have:
The main function is:

To move the graph vertically we have:
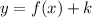
If
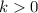 , the graph moves k units up
, the graph moves k units up
To move the graph horizontally we have:

IF
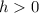 , the graph moves h units to the left
, the graph moves h units to the left
For this case, we want to move the graph k units up and h units counterclockwise. We have then, the following equation:

Therefore, according to the definitions:
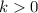
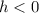
Answer:
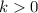
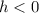
Option: The sign of h must be negative, and the sign of k must be positive.