Question

Identify the vertex and the axis of symmetry of the graph of the function y = 2(x+2)2 - 4

Answer 1

(-2, -4) Would be your answer written in standard form.

Answer 2

Part 1) The vertex is the point
`(-2,-4)`

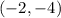
Part 2) The axis of symmetry is equal to
`x=-2`

Explanation:

we know that

The equation of a vertical parabola into vertex form is equal to

`y=a(x-h)^(2)+k`

where

(h,k) is the vertex of the parabola

The axis of symmetry of a vertical parabola is equal to

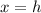`x=h` ----> the x-coordinate of the vertex

In this problem we have

`y=2(x+2)^(2)-4`

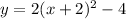
The vertex is the point
`(-2,-4)`

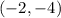
The axis of symmetry is equal to the coordinate of the vertex

so

`x=-2`

see the attached figure to better understand the problem