Question

What are the zeros of the function f(x) = x2 + 8x + 4, expressed in simplest radical form? x = –4 ± 2

Answer 1

a

Explanation:

Answer 2

`x=-4\pm 2√(3)`

Explanation:

We have been given formula of a function
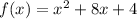`f(x)=x^2+8x+4`. We are asked to find the zeros of our given function in simplest radical form.

We will use quadratic formula to solve our given problem.

`x=(-b\pm√(b^2-4ac))/(2a)`

Upon substituting our given values in above formula we will get,

`x=(-8\pm√(8^2-4*1*4))/(2*1)`

`x=(-8\pm√(64-16))/(2)`

`x=(-8\pm√(48))/(2)`

`x=(-8)/(2)\pm(√(48))/(2)`

`x=-4\pm(√(16*3))/(2)`

`x=-4\pm(4√(3))/(2)`

`x=-4\pm 2√(3)`

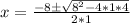
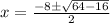
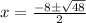
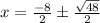
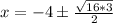
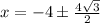
Therefore, solutions for our given equation are
`x=-4\pm 2√(3)`.